GEODETIC ASPECTS OF LAND BOUNDARIES
AND THE PLSS DATUM
IN A
CADASTRAL COMPUTATION SYSTEM
Jerry L. Wahl
Bureau of Land Management
Eastern States Office
350 S. Pickett Ave.
Alexandria, VA
Raymond J. Hintz
Blair Parker
University of Maine
Dept. of Surveying Engr.
Boardman Hall
Orono, Maine 04469
(207) 581-2189
ABSTRACT
Many boundaries and most elements of the Public Land Survey System are
defined in a geodetic sense, for example lines of constant true bearing,
latitudinal arcs, meridians, long straight lines, parallel and other equidistant
lines. This paper will discuss the implications of these definitions, giving
several examples, and discuss the challenge of how to properly deal with
the unique characteristics of such boundaries. This paper will discuss
how this challenge has led to the development of a PC based computational
system for use in the Bureau of Land Management's Cadastral Survey organization.
BACKGROUND
Computational methods
In the current world of surveying there are two widely varying computational
methods in common use. The first method is simple plane survey computations
performed on a local orthogonal coordinate system. Another method in use
for control survey applications uses geodetic computations on a variety
of geodetic systems using spherical or ellipsoidal coordinate systems (latitudes
and longitudes). One common variation of geodetic computations is the use
of any number of coordinate projections or grids.
It is generally understood by surveyors that the use of simple plane
methods while convenient, is not necessarily suitable for large scale surveys.
Why this is so is not usually so well understood. Plane survey computations
have become associated with almost all boundary and construction surveying
while geodetic methods are most often associated with control surveying,
mapping and route surveying. However there are many large scale boundary
surveys where this distinction between computational methods cannot be
maintained. In many large scale surveys it becomes necessary to deal with
some geodetic aspects of the survey. In addition a historical look at the
methods used to carry out such surveys reveals some interesting information
that affects how we must deal with retracing them today.
A good example of a survey system with significant geodetic components
is one used throughout the western United States, the Public Land Survey
System (PLSS). The PLSS was devised in a period of time where survey instrumentation
was limited, yet vast areas of land needed survey. The system was modeled
after a practical survey system that had been used successfully in New
England. The system quickly evolved to a framework of rectangular townships,
often divided into smaller parcels. As the PLSS was prototyped and implemented
beginning in Ohio, it evolved over it's first 50 years. It became quickly
apparent that the term `rectangular' is a generality that cannot effectively
be maintained over a large survey extent.
Cooperative work between Cadastral Survey of the Bureau of Land Management
(BLM), and the University of Maine has resulted in development of an integrated
Cadastral Measurement Management (CMM) software system specific to retracement
cadastral surveys in the PLSS. One of it's design goals was to provide
a set of computational tools that deal properly with these geodetic like
characteristics of large scale boundary surveys. The development of CMM
was necessary because no available software package existed which effectively
worked with this type of information. The following discussion describes
some of these special requirements.
THE PLSS DATUM
The reference system by which the measurements of a system are reported
can be described as a datum. Such a reference system can be quit involved
as in the case of a control survey datum like NAD83, or it can be less
comprehensive. In boundary surveying and retracement it is very important
to gain an understanding of the basis of the measurements reported in the
survey, and in our case we are concerned with what this reference is for
the PLSS. This reference for measurement and reporting will be referred
to as the PLSS Datum. The data being reported on a current Bureau
of Land Management (BLM) or older Government Land Office (GLO) Cadastral
Survey plats are bearings and distances. But what are these bearings and
distances in reference to? The datum that surveys of the PLSS have been
reported in for over 200 years is discussed in various sections of the
Bureau of Land Management's current guide, The Manual of Surveying Instructions,
1973, as summarized below.
Reference to Manual Sections
- 1-3. "Details of the plan and its methods go beyond the scope
of textbooks on surveying. The application to large-scale area requires
an understanding of the stellar and solar methods for making observations
to determine the true meridian, the treatment of the convergency of the
meridians, the running of the true parallels of latitude, and the conversion
in the direction of lines so that at any point the angular value will be
referred to the true north at that place."
2-1. "The law prescribes the chain as the unit of linear measure
for the survey of the public lands. All returns of measurements in the
rectangular system are made in the true horizontal distance in miles, chains
and links...."
2-17. "The direction of each line of the public land surveys
is determined with reference to the true meridian as defined by the axis
of the earth's rotation. Bearings are stated in terms of angular measure
referred to the true north or south."
2-19. Describes 3 Basic methods practices used to determine true
bearings, 1) Direct Sun, star or polaris observations; 2) Solar attachment;
3) Angles from the horizontal control network. Use of the gyro-theodolite
is also mentioned.
2-74. This entire section is very important in describing geodetic
implications of the PLSS datum. It describes in detail methods for carrying
forward true bearing, and defines the term mean bearing and many other
critical concepts. ".... By basic law and the Manual requirements,
the directions of all lines are stated in terms of angular measure referred
to the true north (or south) at the point of record."
2-76. Defines the solar method for laying out the true parallel of
latitude.
2-79. Contains formulas for computing Convergency of two meridians,
corrections to closure computations as a factor of area, and computing
Rb, effective radius of a parallel.
2-80. Describes use of the Standard Field Tables to determine convergency
and other geodetic effects.
2-81,82. Describe the use of M and P factors for converting measurements
to differences in latitude and longitude. A simple version of geodetic
computation.
3-87. Subdivision of Sections: use of the term "straight lines".
5-25. Double proportion - 'Cardinal equivalents to be used, and cardinal
offsets made to determine final point.
5-31. Single Proportion: correction for latitudinal curve.
5-36. Other adjustments to allow for curvature.
These references as well as those in other BLM and GLO Manuals make
it clear that we can define the PLSS datum with the following observations.
Distances: The frame of reference for distances is defined as
horizontal measure in chains based on the U.S. Survey Foot at actual
ground elevation. This is true because measurements were made along
the ground with reduction to horizontal only. With a chain length of from
2 poles to 5 chains this effectively follows the terrain.
Bearings: The frame of reference for direction in the PLSS as
something called Mean True Bearings referenced to the true
meridian "... at the point of record". There is a small
ambiguity in this definition, in that there is a slight difference between
a geodetic azimuth and an astronomic azimuth that has generally been neglected
considering the overall accuracy and instrumentation used.
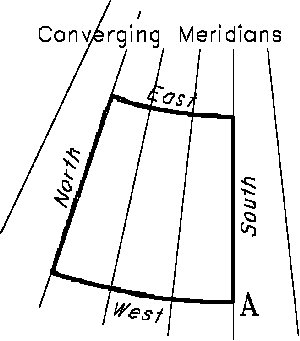
Figure 1: Lines on exagerated converging
meridians.
Those familiar with basic geodesy will recognize that this is a basis
of bearing that is not orthogonal. In one way of thinking it is a reference
that changes as you go east and west because these reference meridians
are not parallel but converge towards the pole.
Because this is a non-orthogonal reference the direction of a straight
line on the ground can be described with a forward bearing based on the
meridian at the beginning point, or by a different back bearing based on
the meridian at the end point. The difference between these is the angle
of convergency of the meridians through those end points.
To visualize this refer to Figure 1, which illustrates a simple
model of the bearing datum with meridians converging as you go north. A
straight line from Point "A" to the right to point "B"
on the left (line 1), crosses each meridian at a differing angle. The angle
with a meridian is the true bearing at that point. More on this later.
To describe how far north or west the line goes in a geodetic sense,
the average or 'mean' of these two values is used. This mean bearing
is essentially identical to the bearing of the straight traverse line with
reference to it's midpoint. Thus the point of record for determining
the bearing of a traverse line can be said to be the meridian at the midpoint
of the line.
IMPLICATIONS OF THE PLSS DATUM
Straight Lines
A straight line for our purposes is what most people would think of
as a straight line. It is the same as a line of sight, or a line laid out
by double centering. In a purist geodetic sense a long double-centered
line is not exactly straight due to small variations in gravity as well
as the effects of travelling along an near elliptical surface. Over very
long lines we would end up with a slightly wavering line called a geodesic.
For practical considerations in the PLSS however a line of sight is a straight
line. The first unusual byproduct of the PLSS datum is:
- I. Straight lines on the ground are lines of constantly
changing bearing.
This is true because such a line will pass each converging true meridian
at a different angle. (Unless it is a due north and south line which goes
along the meridian.)
An example of a boundary that might be straight is one described as
a straight line running from one physical monument or point to another.
The South boundary of California (with Mexico) and the diagonal eastern
boundary between California and Nevada are examples. Such a line if reported
in the PLSS Datum would have considerably different forward bearing and
back bearings as well as different bearings at each point along it. This
is illustrated by line 1 in Figure 1, between points "A"
and "B". This line has a forward bearing at "A" of
WEST, it departs at right angles to this meridian. As one moves along the
line to the west it crosses each meridian an a stronger angle going farther
and farther to the southwest. The back azimuth is the angle with the meridian
at point "B".
Lines of constant bearing
The actual methods and instruments that were used to lay out many survey
lines determined bearing at frequent intervals with reference to the converging
meridians, and were thus run at a constant bearing.
Many boundary lines in the PLSS are in fact lines of constant true bearing.
Another term used in navigation is a rhumb line. It is important
to realize that these lines are NOT straight lines as they cross
every meridian at the same angle and thus appear curved as viewed on the
ground. Therefore:
- II. Lines of constant bearing in the PLSS datum
will be `curved' on the ground.
The magnetic compass, solar compass and solar transit determined true
meridian at each setup. When this type of instrumentation is matched with
traditional chaining of the lines they laid out lines of constant bearing
which are therefore curved.
The `Manual' discussion of latitudinal arcs illustrate one example
of a rhumb line. A parallel of latitude is a line that is due East and
West in the PLSS Datum. Such a line must cross each meridian at a 90 degree
angle in order to have a mean bearing of East or West. An example of such
a line is illustrated by line 3 in Figure 1. This line crosses each
meridian at right angles, and is also a parallel of latitude. A line of
constant bearing between point "A" and "B" is shown
as line 2. It also crosses each meridian at the same angle. It is nearly,
but not exactly, a circular curve. All lines of constant bearing in the
PLSS datum except meridians will appear curved on the ground.
Chords to the arc
Since survey instruments more easily deal with straight lines and traverse
lines are straight lines, a useful concept to keep in mind is that:
- III. The mean bearing of any chord or sub-chord
connecting any two points along a PLSS rhumb line will be the same as the
bearing of the rhumb line itself.
This is illustrated by examining the straight line `chords' c1, c2,
c3 and c4 shown in Figure 1. If these were traverse lines
corrected to mean bearings, their endpoints fall along the curved line
being run. Thus it is possible to lay out points on a rhumb line by correcting
each traverse line to it's mean bearing in computations. It can be seen
that the midpoint of each of these lines is at right angles to that meridian
and therefore have a mean bearing of East and West.
Most PLSS boundaries are RHUMB lines or lines of constant bearing.
This includes standard parallels, township exteriors, section lines, many
grant and reservation lines. Other examples include many state lines, the
U.S. - Canada border, etc.
Some boundaries are straight lines. This includes specifically
described portions of grant or reservation boundaries, some portions of
state lines. Subdivision of Section, (see Section 3-87 of the Manual).
Closure
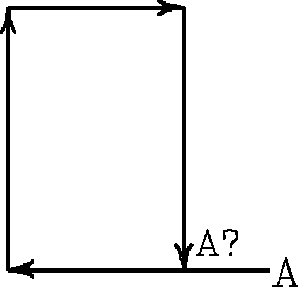
 Another phenomenon
arises when we attempt to compute traverses in this datum. To illustrate
this see Figure 2. The figure shown overlaying the exaggerated converging
meridians is what could be called a "cardinal square". It is
a figure which has its sides bearing West, North, East and South by true
meridian bearings. In this case let us say that the South, West and East
lines are all 5280.00 feet in length. It is apparent from the illustration
that the north line must be shorter due to the convergency of the meridians.
Another phenomenon
arises when we attempt to compute traverses in this datum. To illustrate
this see Figure 2. The figure shown overlaying the exaggerated converging
meridians is what could be called a "cardinal square". It is
a figure which has its sides bearing West, North, East and South by true
meridian bearings. In this case let us say that the South, West and East
lines are all 5280.00 feet in length. It is apparent from the illustration
that the north line must be shorter due to the convergency of the meridians.
How much the meridians converge is a function of the particular latitude,
it being larger the farther north in latitude one goes (in the northern
hemisphere).
At a latitude of 40ø at about the middle of the continental U.
S., the north line of such a `square' would be 1.12 feet shorter. At a
latitude of 70ø in Alaska the line would be 3.65 feet shorter.
Figure 2. A cardinal "square" (above right)
If we were to take these lines and attempt to compute a closure, we
would see something like the diagram shown in Figure 3. As you can
see one does not appear mathematically to return to the place of beginning
even though this is a perfect geometric figure. This apparent misclosure
is in easting only.
Figure 3 - How the data would close... (below left)
This leads to another observation:
- IV. A theoretically perfect survey will appear
to misclose in the PLSS datum.
This effect will be called `apparent misclosure due to convergency
of the meridians'. It is a function of latitude and the area of the
loop being closed.
Due to this apparent misclosure a computation of coordinates for a point
through traverses will produce a different coordinate value for each path
taken . The values will depend on the area between the path to the point
and a true line directly to the point. The only correct answer is one obtained
by running the straight line to the point. Coordinates systems based on
mean bearings will always have difficulty because the math and trig functions
we are tempted to use is based on an orthogonal coordinate system, and
we are dealing with a different shaped system.
Elevation
The distances in most surveys are reduced to horizontal, but are often
not to any other surface. This is true in the PLSS datum as well. Because
of this the elevation of the actual lines sometimes becomes relevant in
a computation. For example, if the north boundary of a township varies
3000 feet in elevation along it's length, care must be taken in the method
used to proportion lost positions for corners along it. This is not a problem
when proportioning against a retraced line run over the same area, but
could be a problem if, for example, the data had been reduced to a grid,
or to `sea-level' latitudes and longitudes before being proportioned. In
essence, elevation can be a weighting factor if reduced measurement data
is used for the proportion.
SPECIAL BOUNDARY RESTORATION ADJUSTMENTS
In the PLSS a number of specialized corner restoration processes have
evolved. Among these are, single and double proportion, the irregular boundary
adjustments, the non-riparian meander line adjustment and the grant boundary
adjustment. Descriptions of these methods are outlined in Chapter 5 of
BLM's Manual of Surveying Instructions, 1973. All of these methods
have important elements that involve the geodetic nature of the PLSS. For
example, a correction for latitudinal arc is mandated on single proportions
and on East-West irregular boundary adjustments. Double proportion also
requires proper consideration for true north in order to be properly performed.
Few, if any software packages available include any of these restoration
methods at all.
CADASTRAL MEASUREMENT MANAGEMENT
The unusual nature of the PLSS datum creates many challenges to a computational
system. As mentioned above, Cadastral Survey, Bureau of Land Management
(BLM) in cooperation with the University of Maine has developed an integrated
computational system that deals properly with the geodetic affects discussed.
The software system is called Cadastral Measurement Management or
CMM for short. It contains a comprehensive set of tools to perform
functions in the PLSS datum. For example:
CSTUF CMM contains a geodetic computation program called CSTUF
which provides many computations using plane, geodetic forward or geodetic
mean bearings. The computations within the system are mostly geodetic but
results are stored as state plane coordinates in CMM. An example of the
necessity for such a package is illustrated by line 4 shown in Figure
1. This illustrates a potential computation of an intersection between
a boundary defined by a straight line, and one defined by a line of constant
bearing. Use of a traditional computational system would result in the
intersection of two straight lines, which can be considerable in error
to the north of the correct intersection. CSTUF provides many other features
including all forms of intersection computations, mean bearing traversing
and inversing. In addition it contains a macro capability that can store
and replay computations.
ADJUST The specialized boundary adjustments required for PLSS
retracement work are handled in CMM by several programs. The program ADJUST
provides manual solutions to single and double proportioning, but in addition
is the primary tool for computation of 1, 2 and 3 point control restoration
methods, the irregular boundary adjustment and the grant boundary adjustment.
Like CSTUF, it also includes macro capability to allow storing a problem
for recomputation.
PROPORT The CMM program proport is a more automated means to
compute single and double proportions. If a project requires a number of
such computations, this can become quit time consuming to do with ADJUST
as the record must be entered again for each computation. PROPORT makes
use of a file which must be created by the system user that reflects the
plat being proportioned. Once constructed and verified, this file is used
by several CMM programs to allow quick computation of proportions. Even
for a single corner, a proportion may be computed a number of times, first
to determined search areas, then to evaluate evidence as it relates to
the record, and as other controlling corners are recovered the proportions
often need to be recomputed based on current status of found controlling
corners.
AUTOPROP An even more automated proportioning utility is also
provided in CMM. As with PROPORT this system requires a plat record data
file to function. It is then capable of proportioning all normal lost section,
1/4 section, 1/16th section corners and subdividing all normal sections
very quickly. The primary reason for this program was to provide corner
search coordinates that can be quickly updated as evidence is found and
evaluated for controlling PLSS monuments. Another CMM utility is then used
to flag traverse points that represent controlling monuments, then AUTOPROP
will quickly compute the rest of the points.
CMOVE CMM also contains a basic utility to compute what are called
corner moves or `ties'. After the final data is derived and all missing
corners have been determined or reestablished then CMOVE provides the ability
to compute angle, bearing and distance information for setting monuments.
Also true line offsets can be computed.
SUMMARY
The measurement systems used in many large scale boundary surveys and
in particular the Public Land Survey System lead to a number of unusual
considerations which must be dealt with in retracing such surveys. The
lines of the PLSS are described by true mean bearings and ground elevation
distances in what is defined as the PLSS Datum. This datum has a number
of geodetic characteristics which make it difficult to properly work within
with traditional computational methods. These unusual factors lead to the
conclusion that a specialized computational system is required. Such a
system has been developed by Cadastral Survey, Bureau of Land Management
in cooperation with the Survey Engineering Department, University of Maine.
This system, called Cadastral Measurement Management, or CMM, also provides
many unique computational tools that are necessary for retracement work
in the PLSS system and that are not available in any known commercial software
package.
REFERENCES
Blanchard, B.M. (1990), Utility Program Development: A Digitally
Integrated Measurement Management System for the U.S. Public Land Survey
System, M.S. thesis, University of Maine, Orono, ME, 86 p.
Hintz, R.J., Blackham, W.J., Dana, B.M., and J.M. Kang (1988), Least
Squares Analysis in Temporal Coordinate and Measurement Management,
Surveying and Mapping, Vol. 48, No. 3, pp. 173-183.
Hintz, R.J. and C.J. Rodine (1990), Automation and Precision in a
Cadastral Surveying Environment, Proceedings of the ACSM-ASPRS Annual
Convention, pp. 124-133.
Hintz, R.J. and H.J. Onsrud (1990), Upgrading Real Property Information
in a GIS, URISA, Vol. 2, No. 1, pp. 2-10.
U.S. Dept. of Interior - Bureau of Land Management (1973), Manual
of Instructions for the Survey of the Public Lands of the United States
1973, U.S. Government Printing Office, 333 p.
Wahl, J.L. (1990), Cadastral Measurement Management User's Manual,
147 p., Bureau of Land Management, NSPS Board of Governors.
Wahl, J.L., Rodine, C.J., and R.J. Hintz (1991) Progress Report on
the Development of an Integrated PLSS Cadastral Measurement Management
and Retracement Survey Software System.
Cadastral Home | Cadastral
Papers
converted 07/12/96
jl-wahl@access.digex.net
 Another phenomenon
arises when we attempt to compute traverses in this datum. To illustrate
this see Figure 2. The figure shown overlaying the exaggerated converging
meridians is what could be called a "cardinal square". It is
a figure which has its sides bearing West, North, East and South by true
meridian bearings. In this case let us say that the South, West and East
lines are all 5280.00 feet in length. It is apparent from the illustration
that the north line must be shorter due to the convergency of the meridians.
Another phenomenon
arises when we attempt to compute traverses in this datum. To illustrate
this see Figure 2. The figure shown overlaying the exaggerated converging
meridians is what could be called a "cardinal square". It is
a figure which has its sides bearing West, North, East and South by true
meridian bearings. In this case let us say that the South, West and East
lines are all 5280.00 feet in length. It is apparent from the illustration
that the north line must be shorter due to the convergency of the meridians.
