A COMPUTER AIDED DESIGN APPROACH
TO MEDIAN LINE COMPUTATIONS
Jerry L. Wahl
Branch of Cadastral Surveys
Bureau of Land Management
California State Office
2800 Cottage Way, E-2841
Sacramento, California 95825
ABSTRACT
The problem of computing a riparian median line is one that most surveyors
rarely encounter. If, however, you are fortunate enough to work on such
a problem, you quickly find that it is one of the more labor intensive
analytical computation processes in surveying. Evolving technology has
now placed in the hands of the average practitioner tools which can allow
us to more easily and accurately visualize the problem, verify solutions,
and even provide an efficient means to obtain solutions. This paper discusses
the basics of median line computations and describes some of the AutoCad
tools we have developed to simplify accurate median line computations.
GENERAL
A median line is technically defined as a line midway between two shores
or banks. It can be defined by key points, known as salient points, along
the shores, but that method may be a simplification. The problem of computing
a line between two others might seem like a simple geometric problem to
solve, but the actual solution is frequently beyond the tools available
in commercial survey software. In actual practice the result can be a very
complex line that involves many straight and curved segments. This
paper involves a technical exploration of median line computation.
Median lines can be determined for a variety of bodies of water. Some
international and state boundaries in oceans, seas as well as rivers are
determined by median lines. Lakes as well as rivers may have boundaries
defined in them by median lines. Boundaries within relicted bodies of water
are also frequently defined by median lines.
Median line computation has been discussed in a number of papers, primarily
in the application to mapping international boundaries and frequently from
a cartographic rather than survey viewpoint.
PHILOSOPHICAL CONSIDERATIONS
Arbitrariness: Water boundary issues frequently possess a seemingly
arbitrary nature. Seemingly arbitrary, because the truth can only be deduced
or guessed at, or the problem is too complex to deal with. Median line
computations are no exception to this philosophical dilemma in that a very
detailed, complex and precise computation proceeds from rough and crude
base data. For example, we can define the margin of a body of water by
salient points scaled from a 1:100,000 chart, or we can use the record
of an old survey of a meander, or we can perform a new meander, or we can
use large scale photography to deduce all the nooks and crannies along
the shore to the `grain of sand' level. Add to this the fact that you may
be dealing with an historical shore that cannot be measured and only guessed
at, may be a matter of opinion and is frequently disputed.
Certainty: After the base data is agreed upon or stipulated,
there is only one true possible median line solution for that system. The
median `line' may be very complex combination of straight line segments
and parabolic curves, some only a few feet in length. It may be extremely
time consuming to determine and compute so that in the end you may not
find that the complete solution is very convenient.
CONTROLLING ELEMENTS
A median line can be determined in several ways, one that is common
in international law is defined by salient points.
Salient Points. A salient point is a prominent point along the
shore of the water body that has a dominant affect on the median line.
The selection of salient points and the determination of their positions
may seem to be a bit arbitrary, but the solution of the median line for
them is fixed.
Meander Lines. Another way that a median line can be determined,
other than with salient points, is using the meanders. The Manual of
Surveying Instructions, 1973, Section 7-55 states:
"The simplest method of determining the median line is by use
of salient points. This method is of limited application in public land
surveys, where the median line is nearly always determined from the meander
lines."
The general solution for PLSS cases is a meander determined median line.
In the course of investigating a meander determined median line, it became
clear that the salient point solution is a subset of the meander solution.
As in the case of salient points, the data you use for the position
of the meanders may seem arbitrary, but once settled the median line is
set.
ELEMENTS OF A MEANDER DETERMINED MEDIAN LINE
Basic Elements of Meander Lines
Any given point on the median line is controlled by one element on each
of the meanders. These controlling elements are either lines or points.
The points may be salient points or the angle points of meander line. Therefore
the possible controlling conditions are:
Figure 1 (below left)
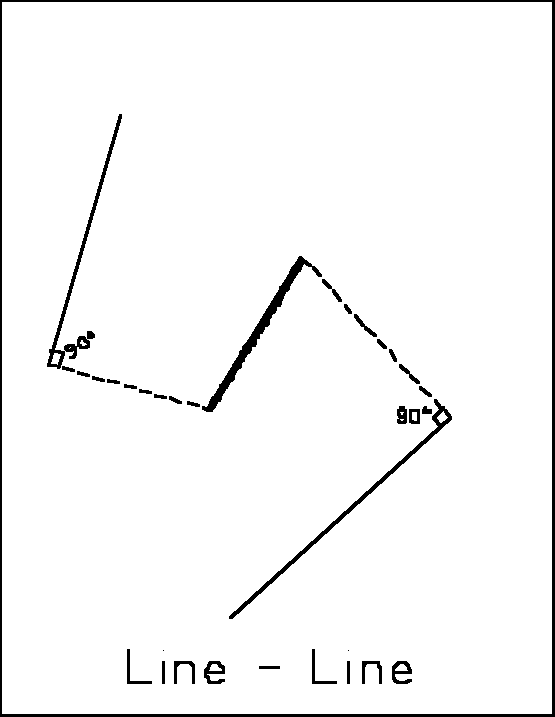 Line
opposite a line. This will be referred to as a Line-Line condition.
The resultant solution for the median line is a straight line midway between
the two banks. This line's position and direction is defined by determining
the angular bisector of the two bank line segments.
Line
opposite a line. This will be referred to as a Line-Line condition.
The resultant solution for the median line is a straight line midway between
the two banks. This line's position and direction is defined by determining
the angular bisector of the two bank line segments.
The condition ends when it intersects another condition or when one
of the controlling lines ends. That point is at the intersection the first
perpendicular from the ends of the controlling lines.
Figure 2 (below right)
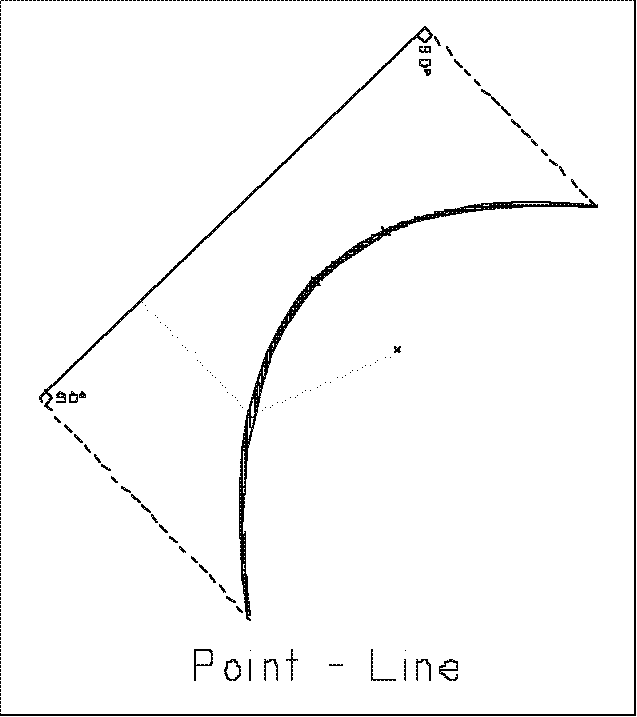 Line
opposite a point. This is the Line-Point condition. The resultant
solution for the median line is a parabolic curve whose directrix is the
controlling line, and whose focus is the opposite controlling point. A
parabola is defined as the locus of points midway between a point (the
focus) and a line (the directrix). Although the Manual seems to
say that these are simple curves, they are not. The condition ends when
it intersects another or when the controlling line ends. That end point
on the median line is at points perpendicular from the controlling line's
endpoint.
Line
opposite a point. This is the Line-Point condition. The resultant
solution for the median line is a parabolic curve whose directrix is the
controlling line, and whose focus is the opposite controlling point. A
parabola is defined as the locus of points midway between a point (the
focus) and a line (the directrix). Although the Manual seems to
say that these are simple curves, they are not. The condition ends when
it intersects another or when the controlling line ends. That end point
on the median line is at points perpendicular from the controlling line's
endpoint.
Figure 3 below left
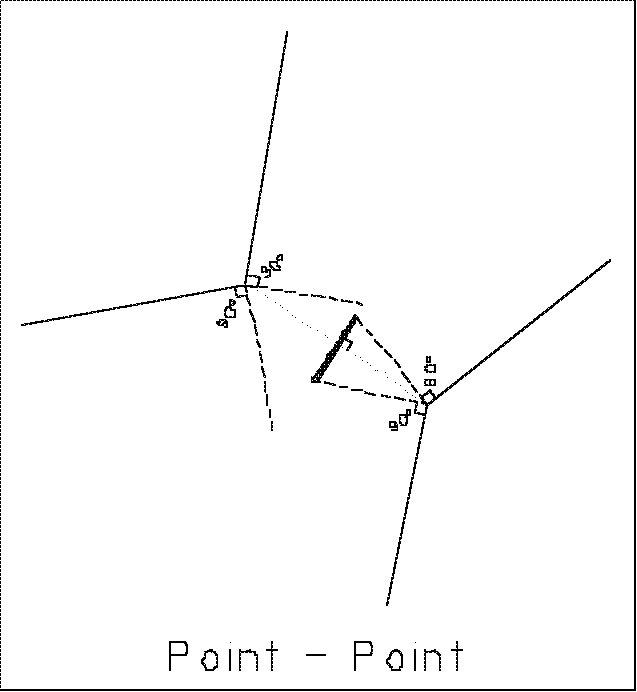 Point
opposite a point. This will be referred to as a Point-Point
condition and it is also identical to a salient point situation. The solution
for the point-point condition is a straight line segment that is a portion
of the perpendicular bisector to a line between the two points. In the
case of a meander determined median line, the condition ends at the first
perpendicular it runs into from one of the lines into the points.
Point
opposite a point. This will be referred to as a Point-Point
condition and it is also identical to a salient point situation. The solution
for the point-point condition is a straight line segment that is a portion
of the perpendicular bisector to a line between the two points. In the
case of a meander determined median line, the condition ends at the first
perpendicular it runs into from one of the lines into the points.
Figure 4 below
 A visual
analogy that can be useful in thinking about a median line is to think
of the median line as the line swept out by the center of a circle of varying
radius travelling down the channel between the two banks. This leads to
the following descriptions of the same conditions.
A visual
analogy that can be useful in thinking about a median line is to think
of the median line as the line swept out by the center of a circle of varying
radius travelling down the channel between the two banks. This leads to
the following descriptions of the same conditions.
The line-line condition can be visualized as the situation where the
circle is rolling between the two lines, increasing or decreasing in size.
The condition terminates when the circle bumps into another line or else
rolls off one of the lines onto an endpoint.
Figure 5 (below left)
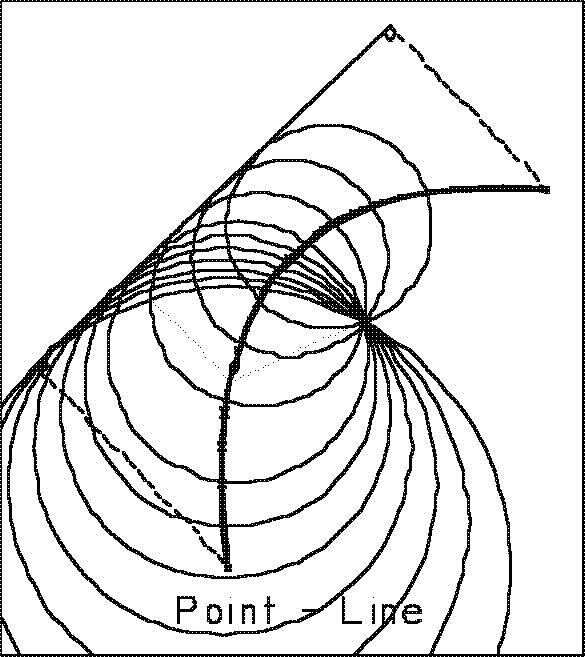 The
point line condition is visualized as a circle pivoting on the controlling
point as it squeezes by the point tangent to the opposite bank. The condition
terminates when the circle bumps into another portion of one of the banks,
or when it rolls off of the point onto one of the lines. That point will
be at the first perpendicular from a line into the point.
The
point line condition is visualized as a circle pivoting on the controlling
point as it squeezes by the point tangent to the opposite bank. The condition
terminates when the circle bumps into another portion of one of the banks,
or when it rolls off of the point onto one of the lines. That point will
be at the first perpendicular from a line into the point.
Figure 6 (below right)
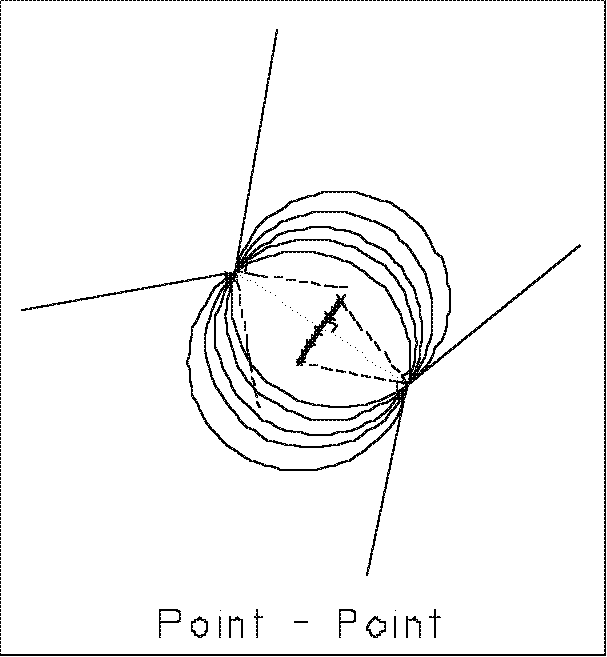 The
point-point condition is visualized as a circle squeezing down between
the two points. The condition terminates when the circle rolls off of the
point and onto one of the lines into the point at the first perpendicular
from those lines.
The
point-point condition is visualized as a circle squeezing down between
the two points. The condition terminates when the circle rolls off of the
point and onto one of the lines into the point at the first perpendicular
from those lines.
Complete Solution. The solution to a median line is simply the
application of the above basics and comes down to determining the proper
controlling condition at any given point along the median line. This seems
fairly easy in the examples shown above, but in actual practice it can
be very difficult.
Determining what the controlling elements are can be deceptive to say
the least. This difficulty becomes more acute the more detailed the meanders
are, or the further apart the banks are in relation to the average meander
length. In addition, the solution is complicated by all the combinations
of intersecting conditions. The combinations are:
- L-L Line intersects L-L Line
- L-L Line intersects L-P Parabola
- L-L Line intersects P-P Line
- L-P Parabola intersects L-P Parabola
The above condition can be the parabolic equivalents to a compound
curve or a reverse curve.
- L-P Parabola intersects P-P Line
- P-P Line intersects P-P Line
The traditional process for developing a median line usually starts
with a sketch drawn to scale. This is done at as large a size as possible
to allow a graphic determination of what appear to be the controlling conditions.
Then by throwing arcs with a compass candidates for possible controlling
conditions are developed. Once that is done, a mathematical solution can
be computed for those candidates. It becomes a process of trial and error.
Sometimes it is difficult to tell exactly what is happening and it is best
to simplify the problem by selecting major points along the meanders rather
than attempting to solve the median in minute detail.
Before now there has only been one primary software tool to do the computation
in the Bureau of Land Management. That is the program developed by William
Ball called WB19. This program computes possible points along the median
line for various combinations of meander conditions. To use it, or any
method, properly it is essential to have identified what condition is being
solved by a method such as discussed in the last paragraph. WB19 then prompts
for entry of the coordinates of all the relevant meander points. Once points
are computed with WB19 they can be plotted back on the sketch and tested
to see if they appear to fall on the median line. More often than not the
test shows that the assumed condition is not correct and additional options
have to be tried until a reasonable looking result is obtained. It is a
trial and error process which can be very time consuming, and a lot of
skill and experience becomes an asset.
Figure 7 (below left)
 In the
summer of 1988, the BLM California Office Cadastral Survey Branch needed
to compute a mile section of river in California. It occurred to several
surveyors there that the use of computer graphics might provide an aid
in the process. At a minimum, it would provide an accurate sketch and eliminate
many of the problems associated with drafting, scaling, the imprecision
in graphic estimating and the problem of multiple erasures coming from
the many trials needed to determine the final set of conditions. Based
on that hope the survey and meander data was keyed in.
In the
summer of 1988, the BLM California Office Cadastral Survey Branch needed
to compute a mile section of river in California. It occurred to several
surveyors there that the use of computer graphics might provide an aid
in the process. At a minimum, it would provide an accurate sketch and eliminate
many of the problems associated with drafting, scaling, the imprecision
in graphic estimating and the problem of multiple erasures coming from
the many trials needed to determine the final set of conditions. Based
on that hope the survey and meander data was keyed in.
CAD as an evaluation tool:
Figure 8 (below right)
 It
was quickly apparent that AutoCad was going to be a big help. Having a
very accurate diagram provided an easy means of testing median point candidates
by throwing circles from them. This simple methodology provided an absolute
check if a point was a valid point on the median line. Examples are shown
in Figure 7 and Figure 8.
It
was quickly apparent that AutoCad was going to be a big help. Having a
very accurate diagram provided an easy means of testing median point candidates
by throwing circles from them. This simple methodology provided an absolute
check if a point was a valid point on the median line. Examples are shown
in Figure 7 and Figure 8.
If the circle intersected the controlling meanders segments exactly,
and no others, then it was proved to be a valid point on the median line.
Because of the zoom capabilities of CAD packages it is easy to determine
if the intersections are close to a degree not possible with a hand drawn
diagram.
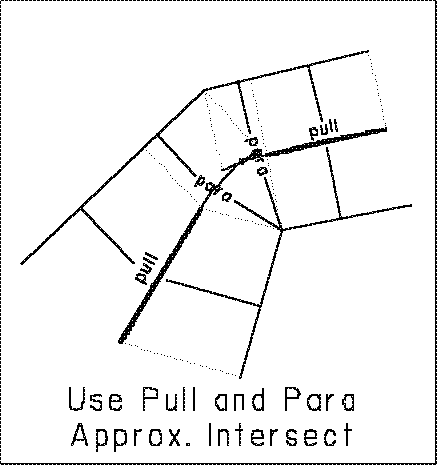
Figure 9
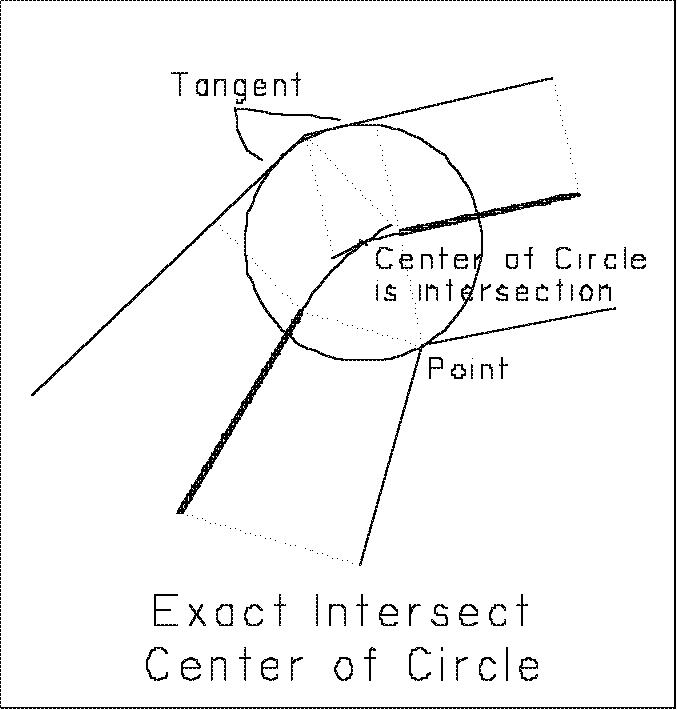
Figure 10
CAD AS A COMPUTATION TOOL
Custom AutoCad Median Line Functions. AutoCad provided the capability
to program new functions. We have made extensive use of this capability
in our plat drafting system. It seemed a logical approach to develop a
few functions to solve at least the more obvious median line situations.
It should also be noted that AutoCad provides very accurate computation
capabilities. And that within the current BLM Cadastral plat drafting system
are functions for bearing-distance line entry, line labelling, grant and
compass adjustments, area computations and many others.
PULL function. The first function developed was for the Line-Line
condition, and the function is called PULL. This allowed quick construction
of many of the straight line segments. Intersections with other line conditions
were obvious and could be derived directly with AutoCad.
PARA function. The next function developed was an aid to construction
of the curved segments. Since these are parabolic curves, which AutoCad
has no direct means to draw, a function called PARA was created
that computes points on a parabola at intervals along the median line and
connects them with short straight segments, in essence small chords. The
user can select the interval to use: long to speedup the process, or short
provide more detail as desired.
This function made it much easier to visualize what was happening with
the curve conditions. For example curve intersecting curve conditions could
be visualized, see Figure 3. It was also apparent that an exact
solution for the curve intersecting anything condition was not always possible
even with this enhanced graphic approach, since the intersection was most
likely to be somewhere along the small chord, rather than on exact parabolic.
This error could become unacceptable when the intersection was with something
at very nearly the same bearing.
MPP Function. Is the Median Point-Point condition function. It
draws a portion of the median line that can be trimmed or extended to it's
proper terminus.
MCHK Function. Median Check. This is a simple routine that just
automates the creating of a check circle by incorporating a few native
AutoCad commands.
DROP Function. Drops a perpendicular from a point to the selected
meander line. This is a simple function that just incorporates a few AutoCad
native commands and is very useful in determining the beginning point for
a new condition after an intersection has been found.
Intersecting Conditions. The exact solution for most of the intersecting
conditions does not actually require a new function. The AutoCad circle
function can accomplish the task by constructing the circle using the `3
point' option, and using what is called `object snap tangent' for those
elements that require it. However, to minimize the number of operations
required to select a such a circle, we have created another shortcut routine:
MINT Function. Median Intersect. Computes intersecting conditions
exactly, after the controlling elements have been determined.
The circle in Figure 10 is an example.
TOTAL SOLUTION WITH AUTOCAD
The AutoCad process involves keying in the section lines with meander
corners. This can be done with coordinates or bearings and distances. Next
the meander lines are entered. They can be adjusted to the meander corners,
if desired. Some thought should be given to what happens to the misclosure
in the section, as different procedures will result in different final
meander lines.
Next, various obvious conditions can be solved, if there are any. Typically
this involves spotting a few line-line conditions. Or just getting started
at one end. By experimenting with moving circles it is possible to make
a good guess at the next condition, then it can be computed and checked.
The process can be thought of as:
- Compute known condition (L-L, P-L, or P-P) to its end.
- Check trial median line section terminus to see if it is a valid point
on the median line. That is, that the median line has not been affected
by intersection with another condition. This can be done quickly by drawing
a check circle.
- If the end point is a valid point on the median line then the case
is one of a consecutive condition, (no intersection). The next condition
is usually obvious, and the process can begin again (with item 1.), or
- If the end point is not a valid median line point, then the case is
one of an intersecting condition. At this point you can usually
figure what condition was intersected by seeing what the circle hit first.
This may involve drawing circles off of prior points generated in the current
condition. Once the next intersection condition is determined, the intersection
can be computed, and the process proceeds accordingly, back to 1.
- Partition lines can be dropped in perpendicular to the median line
from appropriate points. It is a little difficult to precisely drop a perpendicular
to the parabolic curve sections, but it can be done by using the short
chord segments generated by PARA. In the future, perhaps a special exact
function can be programmed for this application.
Sometimes the median line can be so complex that it is necessary to
develop a script of the controlling conditions to keep track of
it.
FUTURE POSSIBILITIES
The use of Autocad following the process described above makes the work
of computing a median line much more efficient. It still requires skill
and knowledge of the conditions in order to properly analyze what the next
condition will be, and what functions to use. On rivers, lakes or other
wide bodies of water it is often very difficult to see what the conditions
will be and the process can be very mentally intense. The CAD approach
provides tools that greatly facilitate this analysis, but human judgement
is still a prime requisite, and the process is still time consuming.
Because the process outlined above is fairly simple with the exception
of the analysis needed to determine what the next condition is in items
3. and 4. If it is possible to formulate the rules properly, it might be
possible to automate the generation of the median line totally. The process
could even be useful even if it were very crude, but if the process is
totally in software, it would still greatly aid in median line computations.
Several potential concepts are on the burner and hopefully we may be able
to implement a fully automated approach this year.
ISSUES
Geodetic Base: If the situation may involve a State Boundary,
probable litigation, etc. it may be advisable to use a well known common
Geodetic base, such as State Plane Coordinates. The exact solution for
the median line will depend on the shape of the projection being used,
as well as the defined controlling lines. This should be considered, and
agreed to by the parties before too much work is done, much as is done
in Outer Continental Shelf Offshore Leasing work.
How Much Detail: With AutoCad it is easier to compute the median
line in complete detail, and it is also possible to easily prove wrong
assumptions. The result is that the final true median line may have a great
deal of detail, in some cases it seems like too much detail. Line and curve
segments only a few tenths of a foot long are not uncommon. Prior to this,
in order to make the job do-able most surveyors simplified the meanders
to avoid such complexity. Again this is not a technical issue, but one
of practicality and judgement.
In my opinion, if the project is likely for litigation, it would seem
advisable to solve the median line completely as this seems to be to be
less arbitrary, can be proven, and thus more defendable in court.
SUMMARY
The geometric problem of computing a median line is an interesting one.
Once base data is defined there is in fact one and only one complete and
correct solution for the median line. With modern tools such as the computer
and CAD software it is more possible and practical than ever to determine
that solution. You may not like it much when you get it though. CAD has
proven to be a valuable tool for use in median line computations. For determining
the conditions, for evaluation of the correctness of answers, and for actual
computation of median lines. Functions have been developed to compute the
fundamental elements and provide checks. In the future it may be possible
to automate the process more completely, and relieve ourselves at last
of the drudgery of this intense computation process.
REFERENCES
The Technical Delimitation of a Modern Equidistance Boundary,
Robert D. Hodgson and E. John Cooper, Ocean Development and International
Law Journal, Volume 3, Number 4.
The Manual of Surveying Instructions, 1973, U. S. Department
of the Interior, Bureau of Land Management Technical Bulletin 6.
Shore and Sea Boundaries, Volumes 1 and 2, Aaron L. Shalowitz,
U. S. Department of Commerce, Coast and Geodetic Survey Publication 10-1,
GPO 1964.
Cadastral Home | Cadastral
Papers
created 07/14/96
updated 07/25/96
jl-wahl@access.digex.net
 Line
opposite a line. This will be referred to as a Line-Line condition.
The resultant solution for the median line is a straight line midway between
the two banks. This line's position and direction is defined by determining
the angular bisector of the two bank line segments.
Line
opposite a line. This will be referred to as a Line-Line condition.
The resultant solution for the median line is a straight line midway between
the two banks. This line's position and direction is defined by determining
the angular bisector of the two bank line segments.  Line
opposite a point. This is the Line-Point condition. The resultant
solution for the median line is a parabolic curve whose directrix is the
controlling line, and whose focus is the opposite controlling point. A
parabola is defined as the locus of points midway between a point (the
focus) and a line (the directrix). Although the Manual seems to
say that these are simple curves, they are not. The condition ends when
it intersects another or when the controlling line ends. That end point
on the median line is at points perpendicular from the controlling line's
endpoint.
Line
opposite a point. This is the Line-Point condition. The resultant
solution for the median line is a parabolic curve whose directrix is the
controlling line, and whose focus is the opposite controlling point. A
parabola is defined as the locus of points midway between a point (the
focus) and a line (the directrix). Although the Manual seems to
say that these are simple curves, they are not. The condition ends when
it intersects another or when the controlling line ends. That end point
on the median line is at points perpendicular from the controlling line's
endpoint. Point
opposite a point. This will be referred to as a Point-Point
condition and it is also identical to a salient point situation. The solution
for the point-point condition is a straight line segment that is a portion
of the perpendicular bisector to a line between the two points. In the
case of a meander determined median line, the condition ends at the first
perpendicular it runs into from one of the lines into the points.
Point
opposite a point. This will be referred to as a Point-Point
condition and it is also identical to a salient point situation. The solution
for the point-point condition is a straight line segment that is a portion
of the perpendicular bisector to a line between the two points. In the
case of a meander determined median line, the condition ends at the first
perpendicular it runs into from one of the lines into the points. A visual
analogy that can be useful in thinking about a median line is to think
of the median line as the line swept out by the center of a circle of varying
radius travelling down the channel between the two banks. This leads to
the following descriptions of the same conditions.
A visual
analogy that can be useful in thinking about a median line is to think
of the median line as the line swept out by the center of a circle of varying
radius travelling down the channel between the two banks. This leads to
the following descriptions of the same conditions. The
point line condition is visualized as a circle pivoting on the controlling
point as it squeezes by the point tangent to the opposite bank. The condition
terminates when the circle bumps into another portion of one of the banks,
or when it rolls off of the point onto one of the lines. That point will
be at the first perpendicular from a line into the point.
The
point line condition is visualized as a circle pivoting on the controlling
point as it squeezes by the point tangent to the opposite bank. The condition
terminates when the circle bumps into another portion of one of the banks,
or when it rolls off of the point onto one of the lines. That point will
be at the first perpendicular from a line into the point. The
point-point condition is visualized as a circle squeezing down between
the two points. The condition terminates when the circle rolls off of the
point and onto one of the lines into the point at the first perpendicular
from those lines.
The
point-point condition is visualized as a circle squeezing down between
the two points. The condition terminates when the circle rolls off of the
point and onto one of the lines into the point at the first perpendicular
from those lines. In the
summer of 1988, the BLM California Office Cadastral Survey Branch needed
to compute a mile section of river in California. It occurred to several
surveyors there that the use of computer graphics might provide an aid
in the process. At a minimum, it would provide an accurate sketch and eliminate
many of the problems associated with drafting, scaling, the imprecision
in graphic estimating and the problem of multiple erasures coming from
the many trials needed to determine the final set of conditions. Based
on that hope the survey and meander data was keyed in.
In the
summer of 1988, the BLM California Office Cadastral Survey Branch needed
to compute a mile section of river in California. It occurred to several
surveyors there that the use of computer graphics might provide an aid
in the process. At a minimum, it would provide an accurate sketch and eliminate
many of the problems associated with drafting, scaling, the imprecision
in graphic estimating and the problem of multiple erasures coming from
the many trials needed to determine the final set of conditions. Based
on that hope the survey and meander data was keyed in. It
was quickly apparent that AutoCad was going to be a big help. Having a
very accurate diagram provided an easy means of testing median point candidates
by throwing circles from them. This simple methodology provided an absolute
check if a point was a valid point on the median line. Examples are shown
in Figure 7 and Figure 8.
It
was quickly apparent that AutoCad was going to be a big help. Having a
very accurate diagram provided an easy means of testing median point candidates
by throwing circles from them. This simple methodology provided an absolute
check if a point was a valid point on the median line. Examples are shown
in Figure 7 and Figure 8.
